Websandbx

Resumé Session 1
Math appliquées à l'informatique

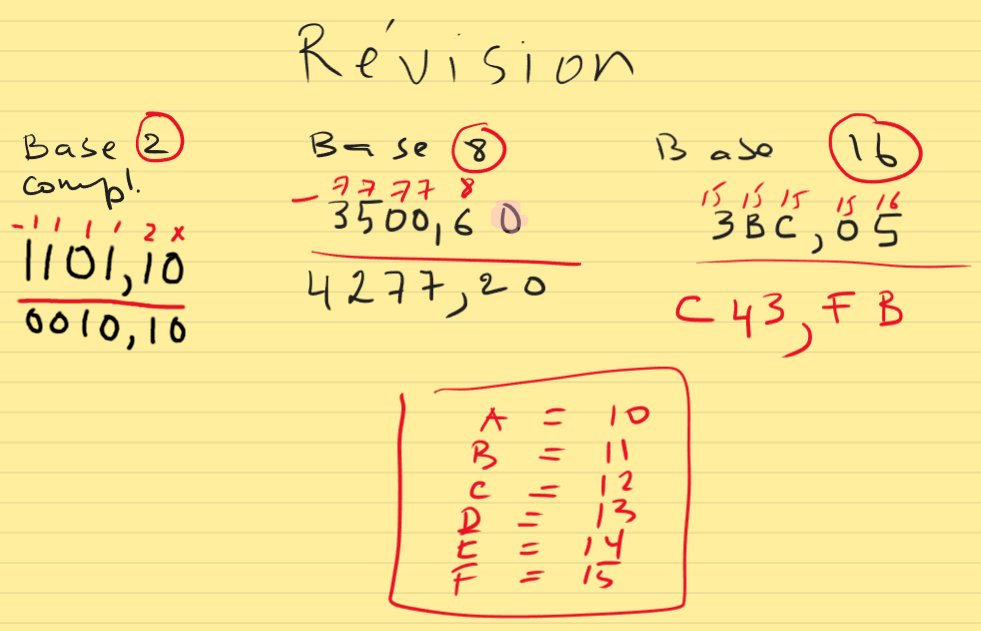
Bases

Partie 1 : Trouver des Bases

ScSh3
ScSh1
Numérotation des Bases

Total de 4 Bases
  • Base 2 (0,1)
  • Base 8
  • Base 10
  • Base 16
ScSh2
Forme Polynomiale
et Somme Polynomiale
  • Forme est celui qui sert a trouver la Base 10
  • Somme est quand on a le 10 et sert a trouver les autres
  • On utilise la position du nombre pour la positionner avec un exposant de la base
  • La position commence toujours par 0 : donc, egale a 1
  • Si c'est inferieur a 0 (virgule), l'exposant sera negatif
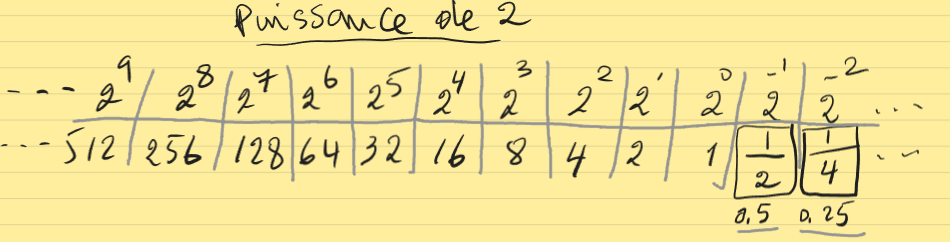
ScSh4
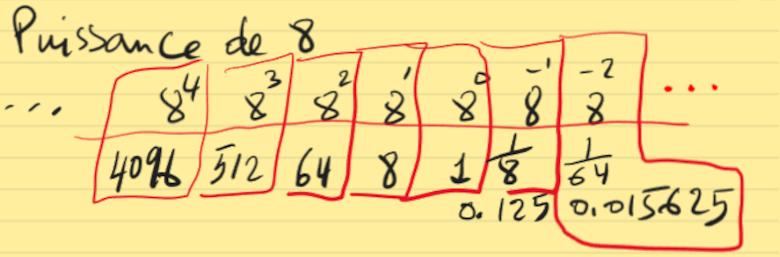
ScSh5
ScSh6
Liste des exposants
  • Pour utiliser avec la somme Polynomiale (Quand on a le 10)
  • Par exemple :
    (11)10 = (23 + 21 + 20) = (1 0 1 1)2
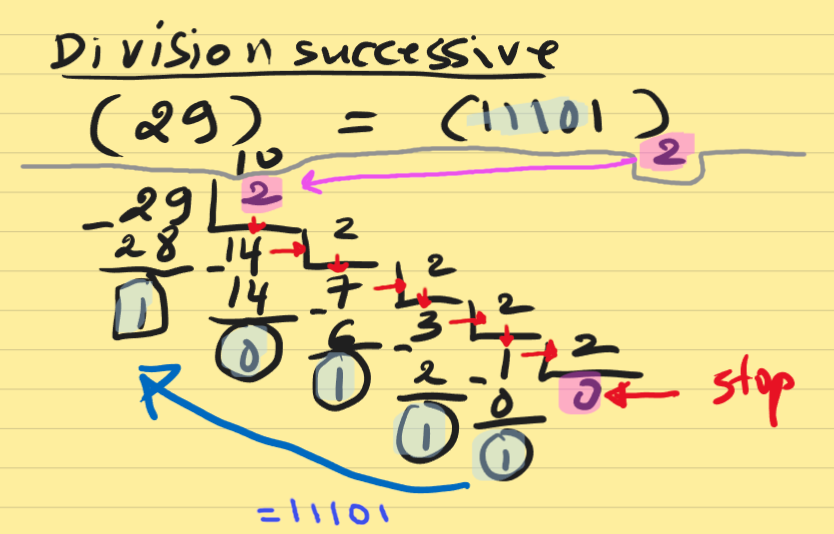
ScSh7
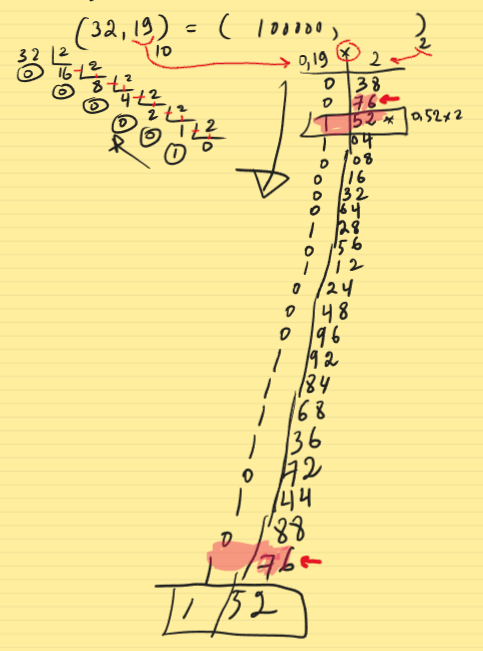
Division successive Multiplication successive ScSh8
  • Besoin de Base 10
  • On divise le nombre du Base 10 par la Base (2,8 ou 16) du nombre Inconnu
  • Seulement pour les numeros apres la virgule
  • Multiplier le nombre par la Base du Inconnue
  • Il est possible d'avoir une repetition, donc cela est une Periodique
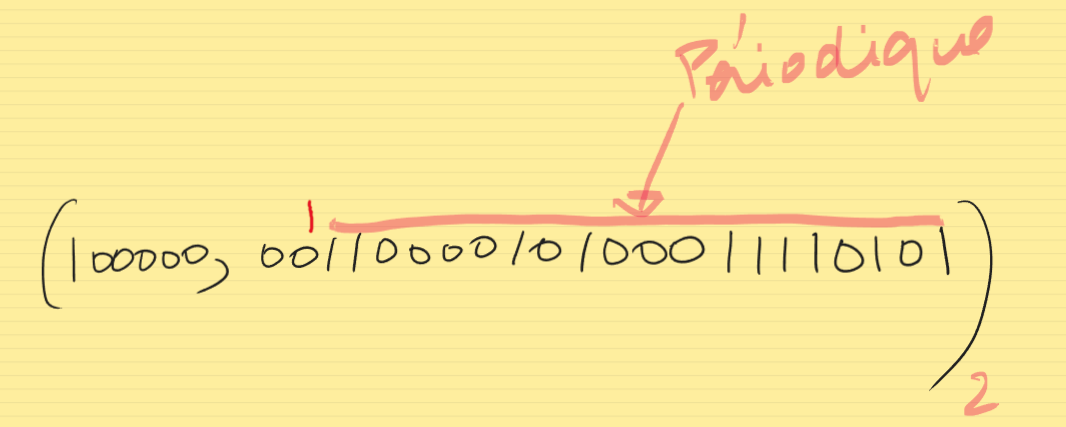
ScSh9

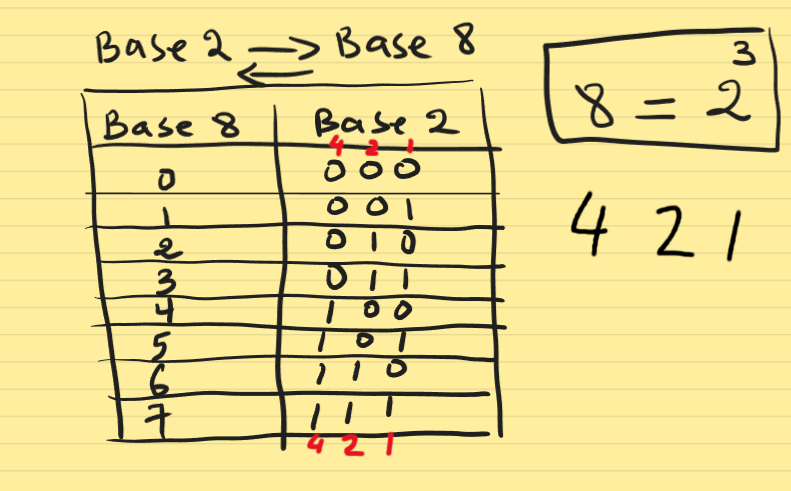
Partie 1 : Trouver la Base 2 avec 8 ou 16

ScSh10
Base2 jusqu'a Base8 (3 positions)
ScSh11
Base2 jusqu'a Base16 (4 positions)

Partie 2 : Additions des Bases

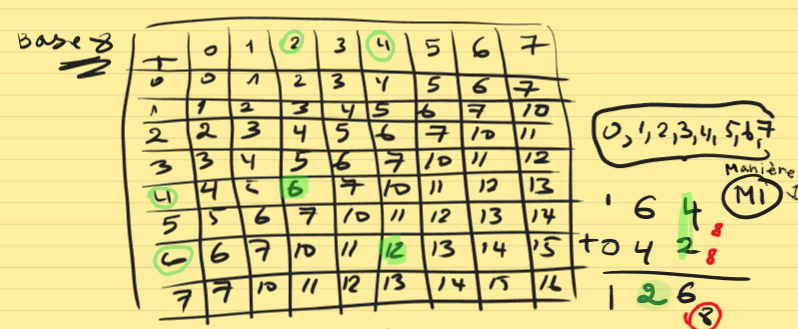
ScSh12
  • METHODE 1 : Tableau (ou addition par coeur)
  • Exemple avec Base8
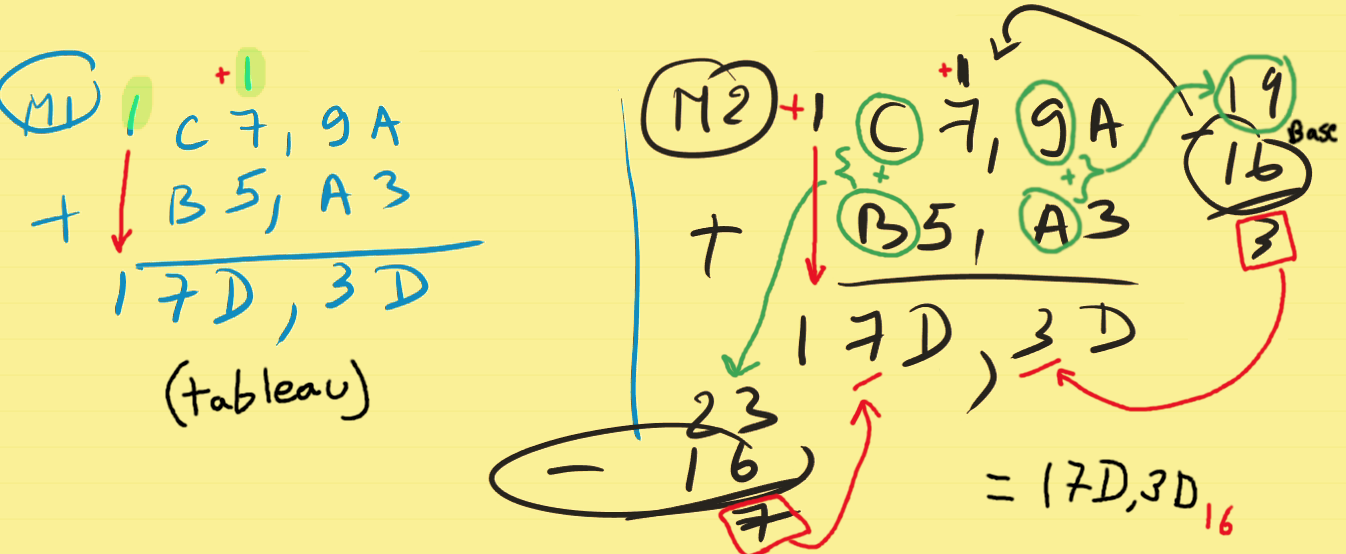
    • ScSh13
  • METHODE 2 : Si l'addition depasse la base,
    on le soustrait avec la base
  • On laisse le reste dans le resultat et +1
    a la gauche de l'addition
    • ScSh14
    Jade Sheet
    ScSh15

    Partie 3 : Soustractions des Bases (Avec complementations)

    ScSh16
    Explication
    ScSh17
    Etapes
    ScSh18
    Comment trouver le complement avec la Base du nombre (Base 10 ici pour simplifier)
    ScSh19
    Trouver le complement avec la Base 2, 8 et 16